Factorización
Así como los números naturales pueden ser expresados como producto de dos o más números, los polinomios pueden ser expresadas como el producto de dos o más factores algebraicos.
Cuando un polinomio no se puede factorizar se denomina irreducible. En los casos en que la expresión es irreducible, solo puede expresarse como el producto del número 1 por la expresión original.
Al proceso de expresar un polinomio como un producto de factores se le denomina factorización.
El proceso de factorización puede considerarse como inverso al proceso de multiplicar.
Factorizar, entonces, quiere decir identificar los factores comunes a todos los términos y agruparlos.
Los factores comunes son aquellos números que aparecen multiplicando a todos los términos de una expresión algebraica.
Estos números pueden estar dados explícitamente o representados por letras.
Así, factorizar un polinomio es descomponerlo en dos o más polinomios llamados factores, de tal modo que al multiplicarlos entre sí se obtenga el polinomio original.
En otras palabras, dada una expresión algebraica complicada, resulta útil, por lo general, el des componerla en un producto de varios términos más sencillos.
Por ejemplo:
2x3 + 8x2y se puede factorizar, o reescribir, como 2x2(x + 4y).
Algunos ejemplos:
De la expresión ab2 + 3cb - b3 podemos factorizar b
y obtenemos la expresión: b(ab + 3c - b2) (1)
Veamos paso a paso cómo se obtuvo la expresión:
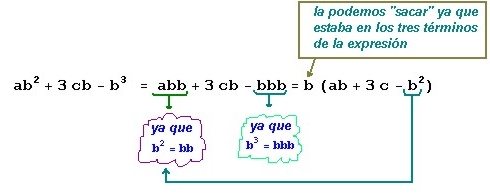
ahora podríamos reacomodar la expresión que queda dentro del paréntesis:
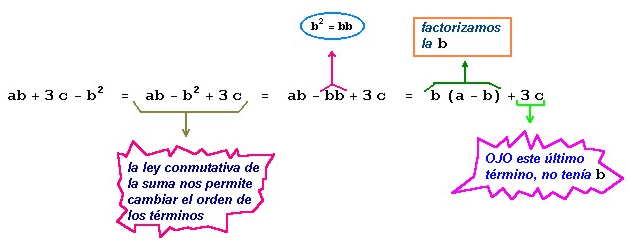
Finalmente si sustituimos este último resultado en (1), obtenemos:
ab2 + 3cb - b3 = b (b (a - b) + 3c)
ab2 + 3cb - b3 = b (ab - b2 + 3c)
ab2 + 3cb - b3 = b (ab +3c –b2)

No hay comentarios:
Los comentarios nuevos no están permitidos.