RACIONALIZACION

RACIONALIZACION

Tratándose de radicales, el proceso de racionalización consiste en eliminar las raíces que se encuentran en el denominador de una fracción.

Dependiendo de las operaciones involucradas dentro de ese denominador pueden presentarse diversos casos:

a) caso en que el denominador contenga una raíz cuadrada, sin adiciones ni sustracciones.

Ejemplo:

Racionalizar: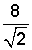 
Como regla general, amplificamos la fracción por el valor de este denominador, en este caso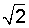  , de la siguiente manera:

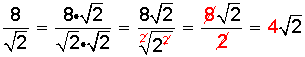
b) Caso en que el denominador contenga una raíz cuadrada, con adiciones o sustracciones.

Ejemplo: 

Racionalizar: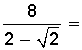 

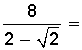
Igual que en el caso anterior, amplificamos la fracción, ahora por 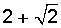, para formar en el denominador una suma por su diferencia (corresponde al conjugado, que es la misma expresión pero con signo contrario), con lo cual dejamos la expresión en:

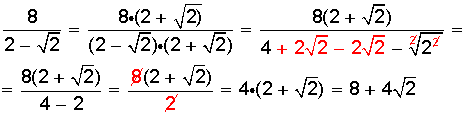
c) Caso en que hay una raíz cúbica en el denominador, sin adiciones o sustracciones.

Ejemplo:

Racionalizar: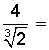 

En este caso amplificamos la fracción por 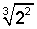, para dejar la expresión del siguiente modo:

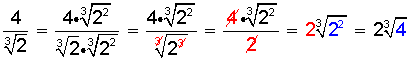
Racionalizar fracciones con radicales en el denominador sirve, entre otras aplicaciones, para ordenar de mayor a menor (para comparar) dichas fracciones.

Ejemplo:

Ordenar de menor a mayor las siguientes fracciones:

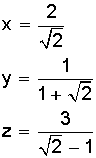
De acuerdo a lo aprendido arriba, racionalizamos cada una de las fracciones:

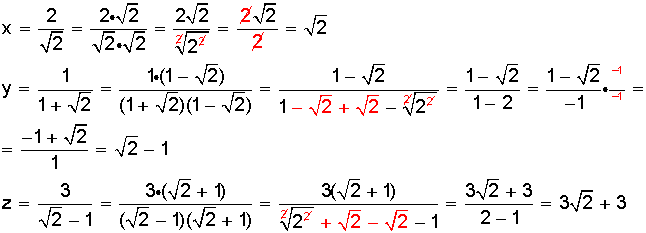
Hecho esto, podemos ordenar de mayor a menor:

RACIONALIZACION DE RADICALES

Cuando tenemos fracciones con radicales en el denominador conviene obtener fracciones equivalentes pero que no tengan radicales en el denominador. A este proceso es a lo que se llama racionalización de radicales de los denominadores.

Según el tipo de radical o la forma de la expresión que aparece en el denominador, el proceso es diferente.

Se pueden dar varios casos:

1. Si el denominador contiene un solo término formado por una sola raíz cuadrada. En este caso basta multiplicar numerador y denominador por la misma raíz cuadrada.

Por ejemplo, si queremos racionalizar el denominador de la fracción , multiplicaremos numerador y denominador por 

Otro ejemplo. Racionalizar 

Si antes de racionalizar extraemos los factores que se puedan en el radical del denominador, tenemos:

Ahora basta multiplicar numerador y denominador por  para eliminar la raíz del denominador:

También se puede directamente multiplicar numerador y denominador por 

Y ahora extraemos factores de la raíz del numerador y simplificamos.

, como vemos da el mismo resultado.

2. Si el denominador de la fracción contiene dos términos en uno de los cuales o en los dos hay una raíz cuadrada, se multiplica numerador y denominador por el conjugado del denominador. O sea si es una suma se multiplica por la resta, y viceversa.

Por ejemplo, multiplicamos numerador y denominador por 

En el denominador siempre va a aparecer un producto de una suma por una diferencia, o sea una expresión del tipo 

Otro ejemplo: , ahora multiplicamos numerador y denominador por 

3. Si el denominador sólo tiene un término con una raíz de índice cualquiera, n, se multiplica numerador y denominador por otra raíz de índice n quecomplete una potencia de exponente n.

Por ejemplo: 

Factorizamos el radicando del denominador: , y como , vamos a multiplicar numerador y denominador por  para completar la potencia de 5

Otro ejemplo: 

Para que se elimine la raíz cuarta, la potencia tiene que estar elevada a 4, luego basta multiplicar por